MassSpringHD app for iPhone and iPad

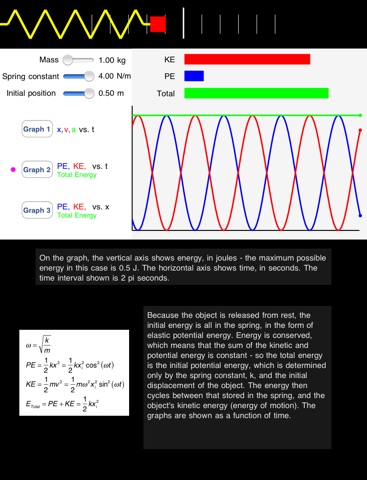
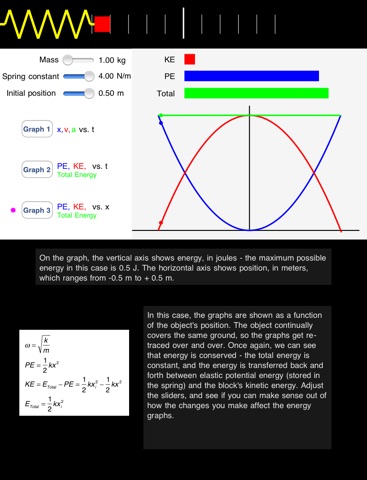
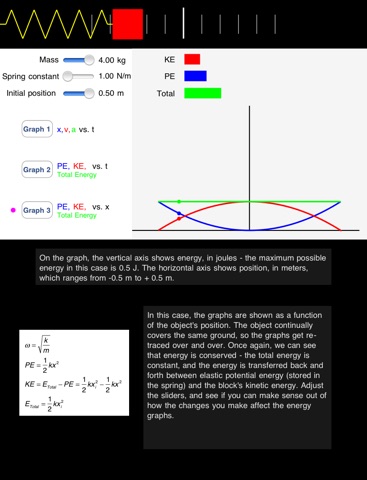
The MassSpringHD app is a basic physics lab, in which a block is attached to an ideal spring. You can set the mass of the block, the spring constant of the spring, and the initial position of the block. The block is released from rest from that initial position, and then oscillates back and forth horizontally on a frictionless surface. This motion is an example of what we call simple harmonic motion. The spring is at its natural length when the block is at a position of x = 0, so nothing happens if you release it from there! On the web site that accompanies this simulation, there is a worksheet, in PDF form, you can use as you work with the app to understand the physics of simple harmonic motion. The worksheet has a collection of equations you can apply as you experiment with the app, and it has suggestions of various activities to do to help you understand how the block and spring system works. The equations are also shown in this app, which is specifically designed for the iPad. Using this app, you can explore various graphs to help you understand what is going on. First, there is a set of three bar graphs that show the blocks kinetic energy (KE), the elastic potential energy (PE) that is stored in the spring, and the total energy (the sum of the kinetic and potential energies). There are also three other graphs – you choose which of these three graphs to display by pressing the appropriate graph button. Graph 1 shows the blocks position, velocity, and acceleration, all as a function of time. Graph 2 shows the kinetic energy, potential energy, and total energy, all as a function of time. Graph 3 shows the kinetic energy, potential energy, and total energy, all as a function of the position of the block. Understanding the different graphical representations can give you various insights into the basic physics of a simple harmonic motion system, as well as into how and why we use graphical representations in the first place. With no friction and no air resistance, this is an idealized system, and you might want to think about what would happen if we were able to add some friction. Idealized systems like this can be a good starting point, though, for getting an overview of how things work.